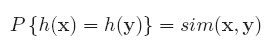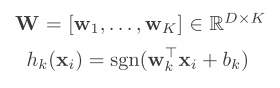Learning to Rank: From Pairwise Approach to Listwise Approach

In the previous paper, support vector learning for ordinal regression, it use pairwise method to solve the problem of ordinal learning. However, using pairwise approach to solve this problem will induce some problem.
First, the objective of learning is formalized as minimizing errors in classification of document pairs, rather than minimizing errors in ranking of documents.Second, the training process is computationally costly, as the number of document pairs is very large. Third, the assumption of that the document pairs are generated i.i.d. is also too strong. Fourth, the number of generated document pairs varies largely from query to query, which will result in training a model biased toward queries with more document pairs.
Thus, in this paper, they propose the list-wise approach.
The followings are the problem setting.

In training, a set of queryies Q=(q⁽¹⁾,q⁽²⁾, ... ,q^(m)) is given.
Each query q^(m) is associated with a list of documents d⁽ⁱ⁾ = (d⁽ⁱ⁾₁, d⁽ⁱ⁾₂, ...,d⁽ⁱ⁾_n(i)).
Each list of documents  d⁽ⁱ⁾ is associated with a list of judgments (scores) y⁽ⁱ⁾= (y⁽ⁱ⁾₁, y⁽ⁱ⁾₂, ...,y⁽ⁱ⁾_n(i)). The judgment y⁽ⁱ⁾_j represents the relevance degree of d⁽ⁱ⁾_j to q⁽ⁱ⁾.
A feature vector x⁽ⁱ⁾_j=ψ(q⁽ⁱ⁾,d⁽ⁱ⁾_j) is created from each query-document pair.
Note that there is a  q⁽ⁱ⁾  in ψ function. If it doesn't have this item, then the ranking list will be always the same no matter what query is.

We want to find a ranking function f, which will output the score by taking one feature vector.
For the list of feature vectors x⁽ⁱ⁾, we can obtain a list of scores z⁽ⁱ⁾ = (f(x⁽ⁱ⁾₁), ... ,f(x⁽ⁱ⁾_n(i))).

The objective of learning is formalized as minimization of the total losses with respect to the training data.

Where L is the loss function.

In order to measure the loss function of two different ranking, they first convert the ranking into probability distribution, and measure the loss function by using Cross Entropy.
They use the following definition to convert the ranking into probability distribution.

However, if we want to derive this probability distribution precisely, we need lots of computation overhead.
Thus, instead of calculating this probability, they calculate top one probability.
Then, for top one probability, the value can be derived more easily.

After using this representation, then we can use Cross Entropy as metric.

And phi-function is defined as exponential function.

Then, they use gradient descent method to solve this optimization problem.
The ranking function f_w is based on the Neural Network model w.
Given a feature vector x⁽ⁱ⁾_j, f_w(x⁽ⁱ⁾_j) assigns a score to it.
Thus, for a query q⁽ⁱ⁾, the score list z⁽ⁱ⁾(f_w) = (f_w(x⁽ⁱ⁾₁), f_w(x⁽ⁱ⁾₂), ..., f_w(x⁽ⁱ⁾_n(i))).
For simplicity, they use linear Neural Network model in the experiment, f_w(x⁽ⁱ⁾_j) = w × x⁽ⁱ⁾_j.
That is, they tried to learn a linear combination that minimize the loss function measure by Cross Entropy.
And they show their list-wise method really performs better than other methods

Support vector learning for ordinal regression

In this paper, they proposed a problem about ordinal regression, which is very different from the traditional learning problems, such as classification and metric regression.

In traditional classification problem, the loss function is defined as 0-1 loss.
In regression estimation, the loss function will take into account the full metric structure.
In ordinal regression problem, the problem this paper want to solve, they consider a problem which shares properties of both classification and metric regression. Like classification, the outcome space is a finite set, and like metric regression, there exists an ordering among the elements.

The detail of the problem is defined as follows.
An input space X belongs to R^n with objects being represented by feature vectors x = (x₁,...,x_n)^T.
Y denotes the rank order.
For every training point in the set S, we want to find a mapping function that map the points to the rankings.

The error cost function is defined as 

l_pref  is 1 if and only if the ranking of h(x1) and h(x2) is different from y1 and y2.
The expected cost can be computed as

However, that is hard to minimize.
Thus, we first convert it into another set S', which is a set representing the pairwise ranking.

And in theorem 1, it said

Which means that for every projection function we get in the set S', the 0-1 loss for S' is proportional to the expected cost for S. Then, the minimum cost projection function found on the set S' will be the same as found on set S.  Thus, now the ordinal problem is converted into the classification problem and can be solved by SVM.

●Solving by using SVM
We want to find a projection vector W, and some biases that project original data into ranks.

Then, we can give SVM some degree of violation, and solve W.

After finding W, we can find different thresholds θ(r_i) for different ranking now by minimizing the following equation under the constraint of above equation.

After doing this, we can get the final results we want as the following figure.

When new data comes, it simply project it by using W, and judge its rank by check the thresholds θ(r_i)

========================================================

Comment:
    The authors are very smart, they convert the ordinal problem into classification problem. Then, they can directly using the methods developed well on classification to solve the ordinal problem. However, I think the most important thing is to tell us why the projection derive on set S' will be the same as S. They only provide a theorem to say that they will be the same but haven't explain it. I think that is one weak point.
    Another weak point is the notation of this paper. This paper use too much equation to define a simple concept, such as l_pref.  I think I will become much better to provide some illustration, or state their meaning directly by using words.

Latent Dirichlet Allocation

Latent Dirichlet Allocation (LDA) is an improved version of pLSI (if you want to check the detail, please click here). Its concept is very similar to pLSI. pLSI tried to learn all possible p(wi|zn), which are the probabilities that word i appears in latent topic n. That is also the same for LDA. However, pLSI has some critical problems. Because pLSI only learns topic mixtures p(z|d) for those documents on which it is trained, there is no natural way to use it to assign probability to a previously unseen document. The other problem is that the number of parameters pLSI needs to learn is kV+kM, which is linear to the number of training document. The linear growth in parameters suggests that the model is prone to overfitting and, empirically, overfitting is indeed a serious problem for pLSI.

LDA solves these problems by treating the topic mixture weights as a k-parameter hidden random variable rather than training a set of individual parameters for each training document.Thus, it only needs to learn k + kV parameters. k parameters for generating the topic mixture weights (α), and kV parameters for β . Furthermore,  the k + kV parameters in a k-topic LDA model do not grow with the size of the training corpus, and will not suffer from overfitting.

The following are the mathematical details.
Assume that given parameters α and β, the joint distribution of a topic mixture θ, a set of N topics z, and a set of N words w is

where p(θ|α) is a Dirichlet distribution.

It's graphical representation is

Then we can get p(w|α, β) by integrating over θ and summing over z.

After that, we can derive p(D|α, β) by multiplying the probabilities p(w|α, β) of all documents appear in the corpus D.

That is the mathematical equation of LDA.

The main difference of pLSI and LDA can be highlighted in the following figure. 

pLSI learns a latent topic combination for every document in the training set. Therefore, the learned combination of one document can be viewed as one point in the above figure. Instead of learning the combination of every document in the training set, LDA tries to learn a distribution to describe the probability that some combination of latent topic appears. That is, it tries to learn a distribution that documents appear in the latent topic space to describe the corpus. 

When new data comes, both pLSI and LDA fix the latent topics and tried to find one point in the latent topic space to minimize the reconstruction error. They need almost the same computational cost to locate the new document in the latent topic space. However, after the document is located, LDA can give one more information then pLSI. LDA can tell us the probability that the new document appears in the current corpus, while pLSI gives every document the same weight and thus cannot tell us that probability.

A Global Geometric Framework for Nonlinear Dimensionality Reduction

The goal of this paper is almost the same as the paper I read last week (Nonlinear Dimensionality Reduction by Locally Linear Embedding). Actually, they are coming form the same year Science magazine, and the position of this paper is one former. The same concept is derived from two different teams at almost the same time. That is quite interesting.

In this paper, they also want to find the low dimension underlying manifold structure from high dimension space.
The example is also "Swill roll".

"A" is the original data structure in high dimension space, and they want to find the underlying structure and expand them as "C".
They also assume that geodesic distance can be approximated by adding up a sequence of “short hops” between neighboring points (This concept is the same as previous paper).
However, they use different method to solve the underlying structure.
They proposed isometric feature mapping (Isomap) algorithm to solve it.The following table is their algorithm overview.

At the first step, they find the neighbor points for every point (the distance of them less then a threshold or found by KNN) . And construct a weighted graph G over the data points by connecting their neighbors.
Every point is viewed as a node in G, and the weight of one edge is defined as dx(i,j). dx(i,j) represent the distance between near points i and j.
After constructing this graph, we can compute the shortest distance of every two nodes by dynamic programming method (Floyd–Warshall algorithm). They denote this distance as dG(i,j).
Then, we know the distances of every two points in the underlying structure. Thus, we can start put them in the new low dimension space. They use classical  multidimensional scaling (MDS) to put the points into d-dimension  Euclidean space Y that best preserves the distances on the graph.
It can be fulfill by minimizing the following cost function.

Where  DY denotes the matrix of Euclidean distances {dY(i,j) = |yi -yj|}.  The Tau operator converts distances to inner products  that supports efficient optimization. This function can be solved by setting the coordinates yi to the top d eigen-vectors of the matrix Tau(DG).
The true dimensionality of the data can be estimated from the decrease in error as the dimensionality of Y is increased. That is shown in the figure below (The true dimensionality of underlying structure is marked by arrows).

They put three experiments result on this paper. For all three data sets, the natural appearance of linear interpolations between distant points in the low dimensional coordinate space confirms that Isomap has captured the data’s perceptually relevant structure.

Nonlinear dimensionality reduction by locally linear embedding

In this paper, the authors want to find the low-dimension representation of the observed data which considers the original data structure. In real world, we receive lots of stimuli at the same time, such as  the pixel intensities of images, the power spectra of sounds, and so on. These oberservations typically have a much more compact description, and are lied on or close to a smooth low-dimensional manifold.  Thus, in this paper, they assume the data are generated on some low-dimension manifold as Fig1 shows.

Traditional method, such as PCA, cannot preserve the distances on the manifold and might lower the performance. LLE (locally linear embedding) wants the find the axes along with the manifold, as figure(c) shows.

Figure 2 is the overview of the algorithm. I will describe them in detail in the following :
For every point, they first find K-nearest neighbors, and use these neighbors to learn the weights which minimize the lose function. (Step 1 in Figure 2)

These weights can be found by solving a least-squares problem.  (Step 2 in Figure 2)
After finding these weights, try to find the low-dimension vector Yi representing the axes on each point.
This can be done by minimizing the following function

That is almost the same as the function in Step 2. The only difference is that the fixed values are Wij now, and we want to find suitable Y. This can be solve by finding the eigenvalues. (Step 3 in Figure 2)
After finding the new positions of all points, we can put all the points on the low-dimension space and the result is like figure 1(c).

They do the experiments on the facial images and text documents, and I only show the result of facial images here.

This figure is generated by projection all the points on the first two coordinates, and the bottom images correspond to points along the top-right path (linked by solid line). We can find the expressions of these facial images change smoothly. That means, this dimension reduction method really somewhat preserves the semantic distances. 

========================================================

Comment:
The authors first observe the behaviors the data. Data often have some correlation between certain dimensions of the high-dim space. That is, data can't expend all the space, and they want to find the underlying structure. They find the distance on the manifold is almost the same as the euclidean distance between near points, and assume this property holds for the data. Then, use this property to resolve the underlying structure. That is a good example for solving the problem by observing the property of the data. 

Probabilistic latent semantic indexing

In this paper, the authors propose one useful method to learn the latent semantic by probabilistic, pLSA.

In pLSA, they model that every document is composed by lots of latent class, and the words generated are only dependent on the latent classes when given latent classes.

So they model the problem like the following.

d represents certain document, w represents certain word, and z is the latent class.

In this paper, they want minimizing the error distance between original data and the reconstructed data after using latent classes (using KL divergence to measure it). After a serious of calculation, we can covert original question to maximize the following log-likelihood function

where n(d, w) denotes the term frequency.

This optimization problem can be solved by using EM algorithm, and the following is the algorithm.

E step:

Calculating the probability of certain class, z, by using the values of d and w get previous round.

M step:

Then, use the P(z|d, w) to update the probabilities of P(w|z), P(d|z) and P(z).

Repeat the steps of E and M until the change rate of results under certain threshold.

The above is the traditional EM method of solving optimization problem. However, the results highly depend on the initial probabilities, and might get the local maximum values by using this method.

Thus, they proposed tempered EM (TEM). This concept is derived from deterministic annealing. Then, the formula in E step becomes that,

The physical meaning of pLSA can be viewed as finding the bases of generating the documents.

P(w|z1), P(w|z2) ... P(w|zn) can be viewed as the basis vectors for representing the document. Because the summation of the values of these bases should be equal to 1, the reconstructed document should be on the plane expended by these vectors. The error rate can be viewed as the shortest distance between the original points and the expended plane. We want to learn a suitable bases that minimize the distance between learned plane and training points.

========================================================

Comment:

I think the most important part of this paper is the physical meaning of pLSA. It is not just a bunch of mathematical formula, optimization, and so on. It also has a very strong physical support that really convinced me which can be used on almost any kind of data, not just an adhoc solution. This paper provides a good example of explaining complex maths in a simple geometric way.

Semi-Supervised Hashing for Scalable Image Retrieval

In this paper, they propose the semi-supervised hashing method. This method solve the problem that unsupervised hashing methods doesn't consider the label of training data, and solve the problem that supervised hashing methods might be over-fitting when training data is small.

They first describe some hashing methods, including LSH, SH, and RBM.

●Locality Sensitive Hashing (LSH)

The main concept of LSH is to map similar samples to the same bucket with higher probability.

This probability can be implemented by random projection.

The following is the function of random projection.

The final hash code is created by concatenating multiple values of random projection functions.

In order to reduce the size of each bucket, K should be large enough.

However, it will also decrease the probability that similar samples fall in the same bucket.

Therefore, we need to use multiple hash tables, and it is inefficient.

●Spectral Hashing (SH)

Because of the inefficiency of random projection, SH appears.

SH try to minimize the following function.

where , k = 1...K

Optimizing this formula is NP-hard, thus it needs to be relaxed.

After relaxing the constraints, the optimization can be solved by spectral graph analysis.

I think that is why it is named "Spectral Hashing".

●Restricted Boltzmann Machines (RBMs)

This method try to learn belief networks by Restricted Boltzmann Machines.

RBMs has two critical stages: unsupervised pre-training and supervised fine-tuning.

The weakness of this method is that it needs to learn lots of weight.

For example, five layers of size 512-512-256-32 modes require to learn 663552 weights.

Therefore, it takes a long time to train.

After introducing three methods, all of them having weakness, they propose their method, semi-supervised hashing.

Let M denote the set of neighbor-pairs, and C denotes the set of nonneighbor-pairs.

Using the information of labeled data, the objective function is try to maximize the following function

Function h_k will only output 1 or -1. Thus, above function try to make the hash codes of neighbor-pairs to be the same, and make the codes of nonneighbor-pairs to be different.

This formula can be rewritten as a matrix format

Let S belong to R^(L*L), we can create the matrix by assigning the following values to each element

And the function becomes

W is the projection planes we want to learn

However, simply maximize this function is almost the same as supervised methods, and it will suffer form over-fitting. Thus, they add the regularization term.

They try to make every single bit hash function outputs the same number of "1" and "-1". That is, maximize the variance of each bit.

This optimization function is also NP-hard to solve again, so they relax the constraint next to solve it. I won't describe the solution details here. If you want to find how to solve it, please read the original paper.

The following is one of it experiments result.

We can find that SSH outperform other methods.

That is the same for the other dataset (gist dataset).

========================================================

Comment:

In this paper, they propose a method between the supervised and unsupervised method. That is a quite smart way to improve the performance. Like most of the thing, best case is often not happened at the extreme points. They often happened in the middle of extreme points. It tells us to think does there exist another problems that are not solved by using the method in the middle of the cases. Then, that might be a good choice for research.