They first describe some hashing methods, including LSH, SH, and RBM.
●Locality Sensitive Hashing (LSH)
The main concept of LSH is to map similar samples to the same bucket with higher probability.
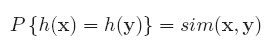
This probability can be implemented by random projection.
The following is the function of random projection.
The final hash code is created by concatenating multiple values of random projection functions.

In order to reduce the size of each bucket, K should be large enough.
However, it will also decrease the probability that similar samples fall in the same bucket.
Therefore, we need to use multiple hash tables, and it is inefficient.
●Spectral Hashing (SH)
Because of the inefficiency of random projection, SH appears.
SH try to minimize the following function.
Optimizing this formula is NP-hard, thus it needs to be relaxed.
After relaxing the constraints, the optimization can be solved by spectral graph analysis.
I think that is why it is named "Spectral Hashing".
●Restricted Boltzmann Machines (RBMs)
This method try to learn belief networks by Restricted Boltzmann Machines.
RBMs has two critical stages: unsupervised pre-training and supervised fine-tuning.
The weakness of this method is that it needs to learn lots of weight.
For example, five layers of size 512-512-256-32 modes require to learn 663552 weights.
Therefore, it takes a long time to train.
After introducing three methods, all of them having weakness, they propose their method, semi-supervised hashing.
Let M denote the set of neighbor-pairs, and C denotes the set of nonneighbor-pairs.
Using the information of labeled data, the objective function is try to maximize the following function
Function h_k will only output 1 or -1. Thus, above function try to make the hash codes of neighbor-pairs to be the same, and make the codes of nonneighbor-pairs to be different.
This formula can be rewritten as a matrix format
Let S belong to R^(L*L), we can create the matrix by assigning the following values to each element
And the function becomes
W is the projection planes we want to learn
However, simply maximize this function is almost the same as supervised methods, and it will suffer form over-fitting. Thus, they add the regularization term.
They try to make every single bit hash function outputs the same number of "1" and "-1". That is, maximize the variance of each bit.
This optimization function is also NP-hard to solve again, so they relax the constraint next to solve it. I won't describe the solution details here. If you want to find how to solve it, please read the original paper.
The following is one of it experiments result.
We can find that SSH outperform other methods.
That is the same for the other dataset (gist dataset).
========================================================
Comment:
In this paper, they propose a method between the supervised and unsupervised method. That is a quite smart way to improve the performance. Like most of the thing, best case is often not happened at the extreme points. They often happened in the middle of extreme points. It tells us to think does there exist another problems that are not solved by using the method in the middle of the cases. Then, that might be a good choice for research.






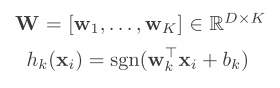



沒有留言:
張貼留言